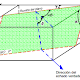
Una función periódica es aquella función en donde sus valores se repiten en intervalos iguales, el tiempo entre las repeticiones(frecuencias) es el periodo. Una función es periódica cuando:
f(t))=f(t+T)
para los valores de t, la constante que satisface la ecuación es el período (T), se mide segundos (s). La parte de la función que abarca un tiempo equivalente a un período T se le denomina ciclo.
 |
| Representación de una onda periódica |
En una función periódica, la frecuencia es la inversa del período "número de ciclos por segundo":
f=1/T
La frecuencia se mide en Hercios (Hz). Un ciclo es igual a 2π radianes, el número de radianes en un segundo es lo que se conoce como frecuencia angular en (rad/s o en 1/s):
Wo=2π/T
La frecuencia y la frecuencia angular son frecuencia pero se miden distinto, considere eso.
Se debe establecer la frecuencia máxima y mínima en un periodo, el valor total es la diferencia de cresta a valle.
F2=Vmáx[f(t)]
F2=Vmín[f(t)]
FT=F2-F1
Ahora se tiene que determinar la frecuencia media de la función periódica:
 |
| J. R. (2021). Ej. de una onda periódica en Matlab. |
- Camilo José Carrillo G. (2003). Fundamentos del Análisis de Fourier. Dpto. de Enxeñería Eléctrica. Universidad de Vigo. Obtenido de: http://grupo_ene.webs.uvigo.es/wordpress/publicaciones/Apuntes_Fourier.pdf
- K. R. Rao (2010). Fast Fourier Transform - Algorithms and Applications. Springer.
